Baeldung - CS

Learn all about Computer Science

Introduction to Differential Privacy in Deep Learning Models
2025-07-25 16:07 UTC by Chizaram Nwachukwu

1. Introduction

In training deep learning models, we use vast amounts of available data, including sensitive information, such as contact details and other personal data. We can mask the sensitive data with traditional anonymization techniques. However, these methods aren’t foolproof, as hackers can decipher anonymized data using linkage attacks.

Differential privacy is an emerging technique that solves this problem without the bottlenecks of traditional anonymization methods.

In this tutorial, we’ll introduce differential privacy, explain how it works, and explore its applications in training deep learning models.

2. Problem Statement

Let’s say we record calls to an emergency response unit. During a routine day, we receive hundreds of calls, collect data, and reroute this information to the emergency services. At the end of the workday, we have a dataset of hundreds of rows.

Now, let’s say we want to build a deep learning model to analyze why certain types of emergencies were recorded in that region within a specific period. This model will access our callers’ records, including Personally Identifiable Information (PII). PII can include our callers’ names, addresses, hospital records, and ages. Traditionally, we’d anonymize this information by obscuring sensitive information or removing the fields entirely.

However, traditional anonymization isn’t enough. Attackers can cross-reference anonymized records with external, publicly available data to identify our callers.

Differential privacy protects against this kind of privacy breach by ensuring that an attacker analyzing our trained model can’t determine whether or not a specific individual’s data was included in our training set. As a result, the attacker can’t reliably infer sensitive information about any targeted person by reverse-engineering the model’s behavior.

With differential privacy, we split the dataset among several models and introduce controlled noise to the models’ training process. The controlled noise during the training obscures the sensitive data. This method of privacy ensures that our model’s analysis remains unchanged even if we add or remove a single record.

3. How Does Differential Privacy Work?

Differential privacy protects individuals’ sensitive data in a dataset by ensuring that the output of any model analysis does not significantly change if one data point is added or removed. We achieve this by introducing controlled noise or randomness into the model’s training process.

Continuing our previous example, we can obscure sensitive data by passing our recorded responses through an algorithm that adds a controlled measure of noise. For instance, we can slightly alter the field that holds the patients’ ages or substitute the addresses with a fictional street or number. Introducing such noise ensures that any record has a negligible impact during training.

In doing so, we can still utilize this data to train our model without compromising security or relevance. Think of differential privacy on data as tuning a device. If we tune to the exact frequency of a radio station, we hear the sounds and music clearly. However, if we add a bit of static noise, we can still hear the sound, but we can’t distinguish any one instrument or identify which person is talking.

3.1. How is Differential Privacy Calculated?

Generally, the idea behind differential privacy is that the probability distribution of a model’s output should remain nearly the same even if we add or remove an individual’s record from the dataset.

Before going to the formula, let’s define the terms:

$\mathcal{M}$ : the mechanism or algorithm (such as a noise-adding function) including the training plus noise
$D_1$ : contains all the data, including the individual’s record
$D_2$ : dataset with all the data except the individual’s record (one record missing)
$S$ : a possible set of outputs from the mechanism. This refers to all possible models or outputs when the trained model is given a specific input, which can be used to test whether an individual’s data was included in the training set. For example, an attacker might input a record and observe the model’s output prediction, expecting the output to differ if the record was part of the training data
$\Pr[\mathcal{M}(D) \in S]$ : the probability that applying the mechanism to dataset $D$ results in an output within $S$
$\epsilon$ : the privacy parameter (also called the privacy budget), controlling the trade-off between privacy and accuracy

Mathematically, we say $\mathcal{M}$ provides the $\epsilon)$ -differential privacy if:

$\Pr[\mathcal{M}(D_1) \in S] \leq e^{\epsilon} \cdot \Pr[\mathcal{M}(D_2) \in S]$

This means that the likelihood of output doesn’t change much whether we add or remove a single individual’s data. The smaller $\epsilon$ is, the stronger the privacy guarantee (due to larger noise), although this typically means our model may have reduced accuracy.

An $(\epsilon, \delta)$ -privacy has an additional parameter, $\delta$ :

$\Pr[\mathcal{M}(D_1) \in S] \leq e^{\epsilon} \cdot \Pr[\mathcal{M}(D_2) \in S] + \delta$

It’s the probability of violating the privacy guarantee. So, if we set $\delta=0$ , we get the so-called pure differential privacy.

4. Challenges With Differential Privacy

One of the major challenges we face when implementing differential privacy is the loss of accuracy, which occurs when we introduce too much noise to protect privacy, thereby compromising the accuracy of the student model.

A higher privacy budget results in lower noise. However, the trade-off is weaker privacy. A lower privacy budget results in high noise levels and stronger privacy, but it also leads to misclassification more often.

Another challenge is the computational overhead due to noise.

Then, there’s the challenge of tuning $\boldsymbol{\epsilon}$ . Typically, industries that handle highly sensitive data, such as healthcare and finance, use stricter privacy budgets.

To address these issues, we can:

Use larger datasets to offset the impact of noise
Optimize batch sizes and gradient clipping parameters to improve efficiency
Employ techniques such as transfer learning, where we first train models on publicly available data before fine-tuning them with differential privacy

5. Implementing a Differential Privacy Framework: The PATE Example

Let’s examine a real-world example where we train models using the Private Aggregation of Teacher Ensembles (PATE) framework. The PATE framework is one of the ways we can implement differential privacy in training ML models. It works well in distributed training systems.

Suppose we have healthcare data shared among different hospitals in a city. The data involves diagnoses based on patient information from various doctors. Here’s an illustration of the PATE framework for this scenario:

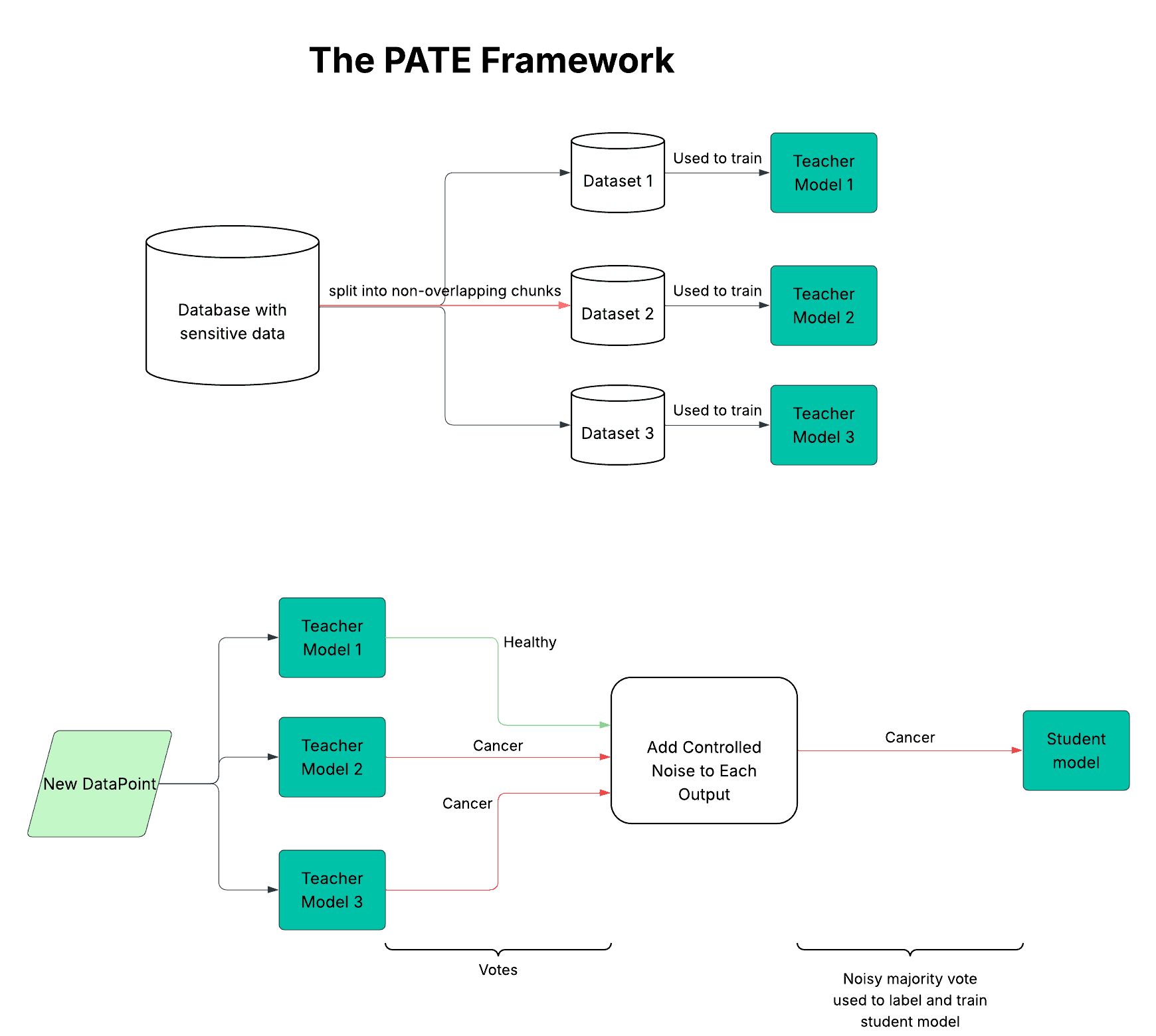
PATE splits the dataset into non-overlapping subsets. Then, the independent teacher models learns directly from these data subsets.

When we want to label a new data point during training, the teacher models vote, and controlled noise is added to each vote. Then, we label the data point with the noisy majority vote, which is then used to train the student model. This way, the student model doesn’t interact with the sensitive data.

5.1. The Teacher Models

In the PATE framework, we always split the sensitive data into non-overlapping chunks and assign them to teacher models. Each teacher model fits its slice learning patterns without access to the complete set.

Looking back at our healthcare scenario, let’s say we have 3,000 X-ray images of lung cancer patients from two hospitals: 1,500 from Hospital A and 1,500 from Hospital B. Using the PATE framework, we shuffle the images and then split them into three non-overlapping groups of 1,000 images each. We train Teacher 1 using the first 1,000 images as input data, Teacher 2 on the following 1,000 images, and Teacher 3 on the final 1,000 images. Shuffling before splitting should make each group representative.

5.2. Introducing Noise

Now, it’s time to get the teachers’ outputs. Each teacher model makes a prediction when we need to label a new data point (such as a new X-ray image). The teacher models vote on the correct label. For example, if two out of our three teacher models vote “cancer” and the third votes “healthy,” the majority vote is “cancer.”

Before the votes are used to label data for the student model, we add noise to the votes through our function. This noise prevents anyone from deducing which teacher model, and by extension, which subset of data, influenced the outcome. The label decided by the noisy majority vote becomes the training label for the student model.

If we have a collection of teacher vote counts $v = (v_1, v_2, ..., v_K)$ for each of the $K$ possible labels, then, for each $v_k$ , we sample noise $N_k$ from a chosen noise distribution, which can either be Laplace or Gaussian (calibrated to the privacy budget), and add it to $v_k$ . Then, the noisy version of that vote, $\tilde{v}$ , is:

$\tilde{v}_k = v_k + N_k$

For example, we can sample $N_k$ from a Laplace distribution calibrated to $\epsilon$ :

$N_k \sim \mathrm{Laplace}(0, 1/\epsilon)$

The output with the highest noisy count ( $\text{argmax}_k \tilde{v}_k$ ) is selected as the label.

5.3. Our Public Student Models

Our student model, which will eventually be deployed publicly, learns from public, non-sensitive data labeled by noisy votes.

This method is effective because our student model doesn’t have direct access to patient data, resulting in a privacy-compliant and accurate model.

6. When to Use Differential Privacy?

Although differential privacy is rapidly being adopted in the data ecosystem, here are the use cases where it is particularly important:

Scenario	Why It Matters	Real-World Example
Sensitive Personal Data (health records, financial info)	Prevents models from memorizing private details	Training cancer detection models on patient X-rays without exposing diagnoses
Collaborative Projects	Enables data sharing without raw data exchange	Hospitals jointly research disease patterns using the PATE framework
Regulated Industries	Provides auditable privacy guarantees	Banks detecting fraud while complying with financial privacy laws
Public-Facing Models	Blocks model inversion and linkage attacks	Chatbots that can’t leak training data containing personal emails
IoT/Sensor Networks	Protects user behaviour patterns	Smart home systems learning energy usage without tracking individual habits

Protecting sensitive data is becoming increasingly important as companies and organizations collect more user information. Differential privacy offers a more effective approach to achieving this than traditional anonymization methods.

Other frameworks are also gaining traction or are widely adopted, such as Differentially Private Stochastic Gradient Descent (DP-SGD), which is supported in libraries like TensorFlow Privacy and PyTorch Opacus. These frameworks offer different approaches to implementing differential privacy, especially in large-scale deep learning models.

7. Conclusion

In this article, we explained differential privacy as a new and improved method for protecting sensitive data during model training. We also discussed how it works, focusing on the PATE framework. Lastly, we explored the challenges of differential privacy and its various use cases.

Differential privacy is a framework that ensures our data remains safe even when it is used to train machine learning models.

The post Introduction to Differential Privacy in Deep Learning Models first appeared on Baeldung on Computer Science.