 Learn all about Computer Science  1. Introduction
Nature often works through simple laws, yet gives rise to unpredictable complexity. Conway’s Game of Life is a computational example of this principle. Developed in 1970 by British mathematician John Conway, this simulation game runs on a grid of cells. Each cell follows basic rules such as live, die, or stay the same based on its neighbors.
Despite this simplicity, astonishing patterns emerge. Stable shapes, repeating cycles, and seemingly intelligent movements evolve from random starting points. The system displays lifelike qualities such as reproduction, mobility, and even interaction between patterns.
In this tutorial, we’ll learn how simple rules can lead to complex, lifelike behaviors through Conway’s Game of Life. This classic simulation is as a foundational example in the study of emergent systems, chaos theory, and artificial life.
2. Cellular Automata
Cellular automata are mathematical models made up of grids of cells. Each cell changes state over time according to a set of rules based on neighboring cells. These models simulate processes in which local actions drive global behavior.
Each cell can have a finite number of states, but there are typically just two: alive and dead. Time advances in discrete steps, and the rule set determines how cells evolve from one step to the next. Each cell’s future state depends only on its current state and the state of its immediate neighbors.
This setup mirrors real-world systems: neurons firing, chemical reactions spreading, and population dynamics evolving. It provides a digital playground to explore how complexity arises from simplicity.
Conway’s Game of Life is the most famous cellular automaton. Others, such as Rule 30 or Langton’s Ant, also demonstrate unique forms of emergent behavior.
3. Conway’s Game of Life Explained
Conway’s Game of Life is a zero-player game that simulates cellular evolution on a two-dimensional grid. Each cell on the grid is either alive or dead, e.g.:
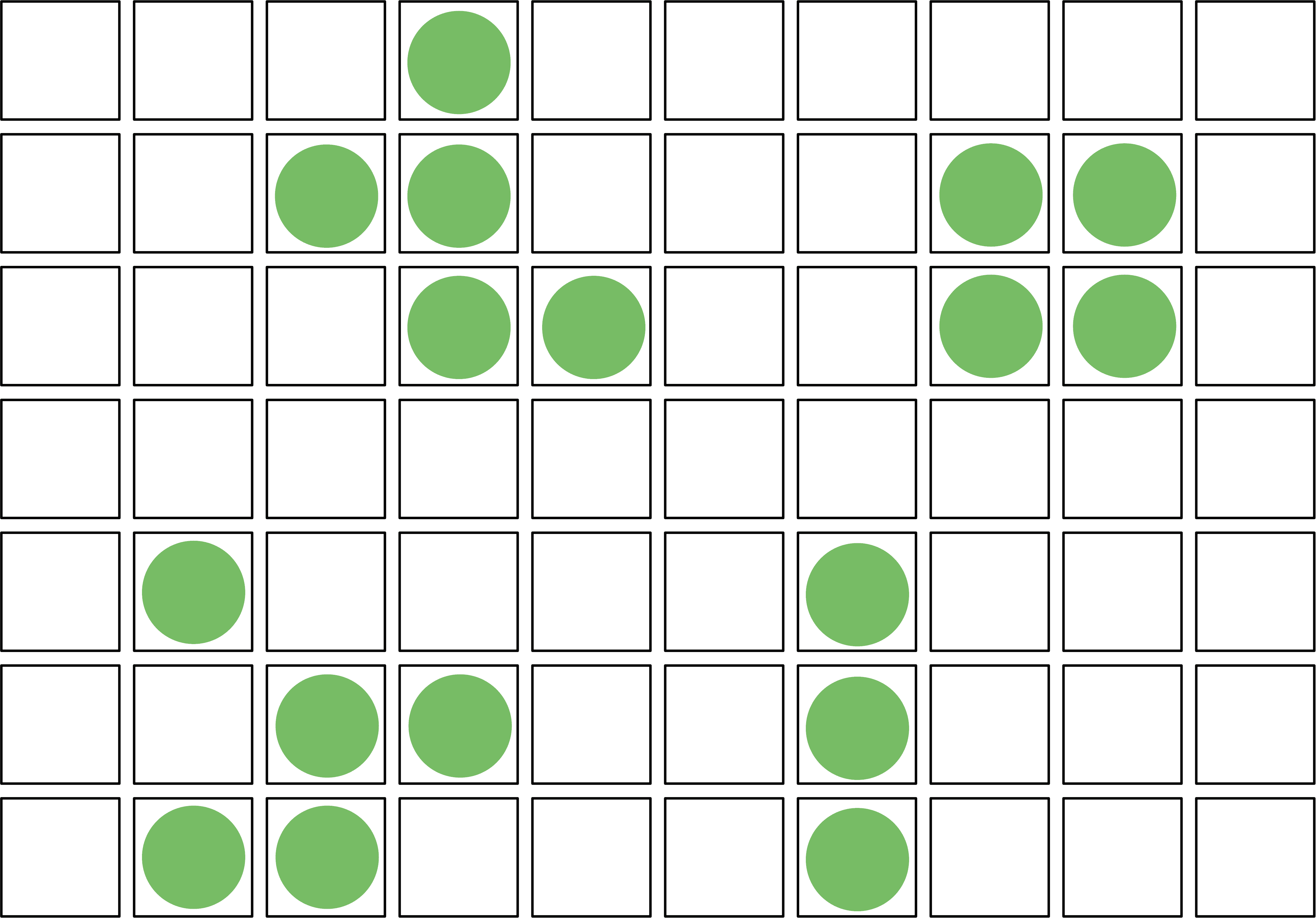
At every time step, cells update based on the number of alive neighbors. The entire system evolves based on just four rules, creating surprising and complex behaviors.
3.1. The Basic Rules of Conway’s Game of Life
Each cell interacts with its eight surrounding neighbors (horizontally, vertically, and diagonally):
- Underpopulation: A live cell with fewer than two live neighbors dies.
- Survival: A live cell with two or three live neighbors lives on.
- Overpopulation: A live cell with more than three live neighbors dies.
- Reproduction: A dead cell with exactly three live neighbors becomes alive.
These rules run simultaneously for every cell at each time step. The state of the entire grid changes in waves, evolving into new patterns with every iteration.
Some patterns are famous for their unique behaviors. These structures demonstrate that the system can store information, transmit signals, and simulate logic gates.
3.2. Still Lives
“Still lives” patterns don’t change over time. Examples are Block, Boat, and Beehive:
These are called “still lives” because all live cells survive (they have 2 or 3 neighbors) and no new cells are born (no dead cell has exactly three neighbors). These patterns are in perfect equilibrium under Conway’s Game of Life rules.
3.3. Oscillators
Oscillators repeat a cycle of states. The simplest is the Blinker, which flips between vertical and horizontal lines:
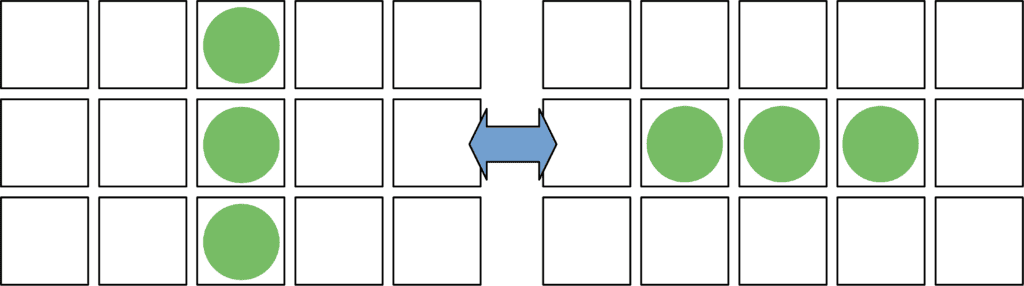
In the horizontal state, the middle cell survives because it has two neighbors, whereas the outer cells have one neighbor each, so they die. The new births occur above and below the center, which flips the pattern to the vertical state. The vertical state then reverts to horizontal using the same logic.
Another example is Toad, which cycles between the extended and compressed shapes:
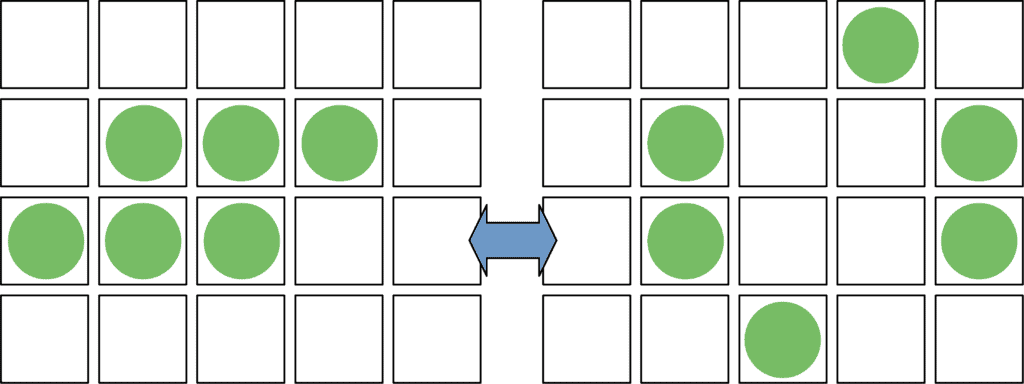
The 6-cell toad structure creates unstable edge conditions, where cells on the edges die and new ones form between the two rows. Each generation alternates the structure’s position. One generation compresses it, the next stretches it.
In a similar way, Beacon alternates between “Corner on” and “Corner off”:
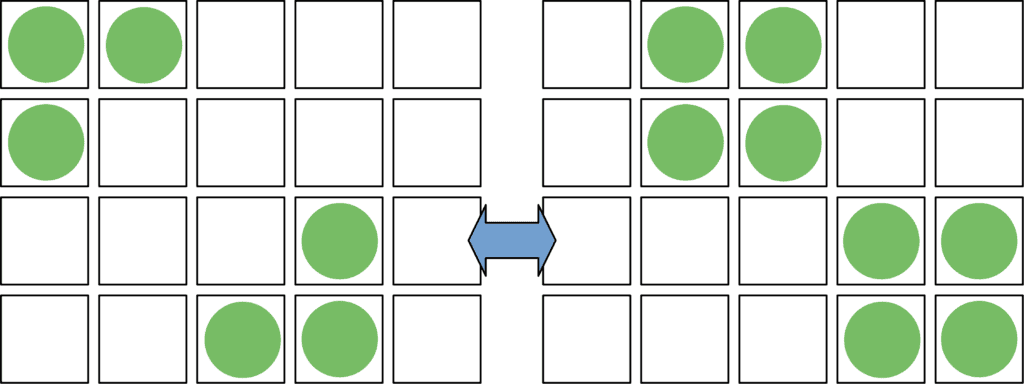
Each of the two sub-blocks (which would be stable alone) interferes with the corner cells of the other. The interaction causes the corner cells to die or be born, flipping between two states. Most of the structure stays the same, only one corner “flashes.”
3.4. Spaceships
Spaceships move across the grid. The most iconic is the Glider, which travels diagonally in a looping motion:
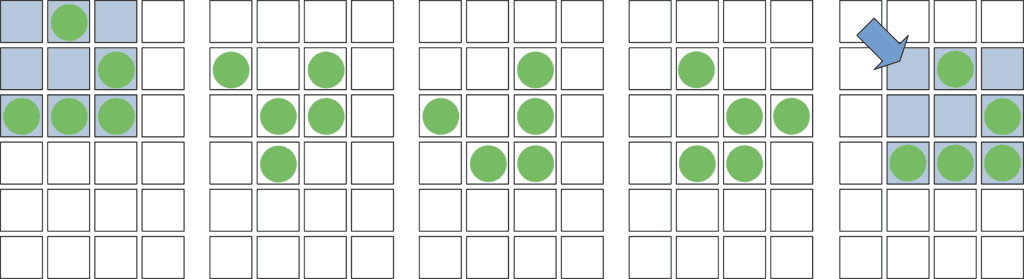
A glider’s arrangement of live cells changes slightly each generation. Over a four-step cycle, the glider returns to its original shape but is shifted diagonally by one cell. This means the pattern is not identical every generation but periodic. It repeats in a loop, just in a new location.
In general, a spaceship doesn’t have to look identical in every step. Instead, it must return to its original shape after a fixed number of steps, but displaced by a specific vector, like one cell right or diagonally.
3.5. Guns
Guns generate other patterns. The most well-known is the Gosper Glider Gun, which produces a stream of Gliders at regular intervals. It was the first known pattern that creates an infinite stream of Gliders, small moving shapes that travel diagonally across the grid:
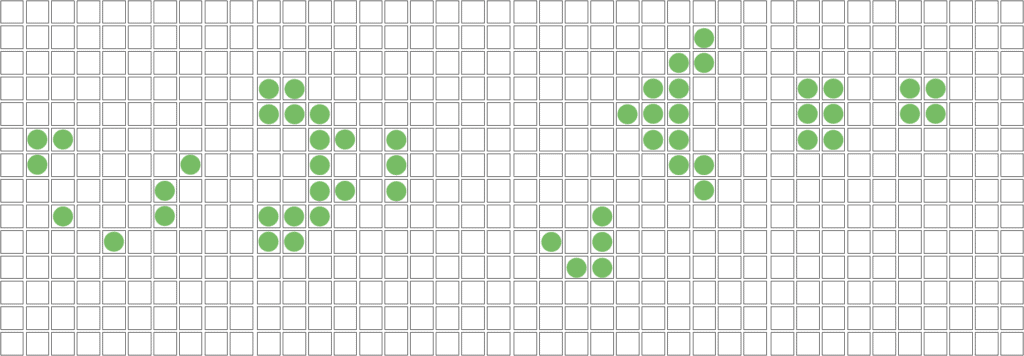
The structure itself is large and stable. Inside it, oscillating cells interact in cycles. Every 30 generations, these interactions release a Glider, effectively turning the system into a repeating pattern generator.
This Gosper Glider Gun is important because it proves that the Game of Life can support patterns with unbounded growth. Before its discovery, all known structures either stabilized or vanished at some point.
This is what we have after a few cycles:
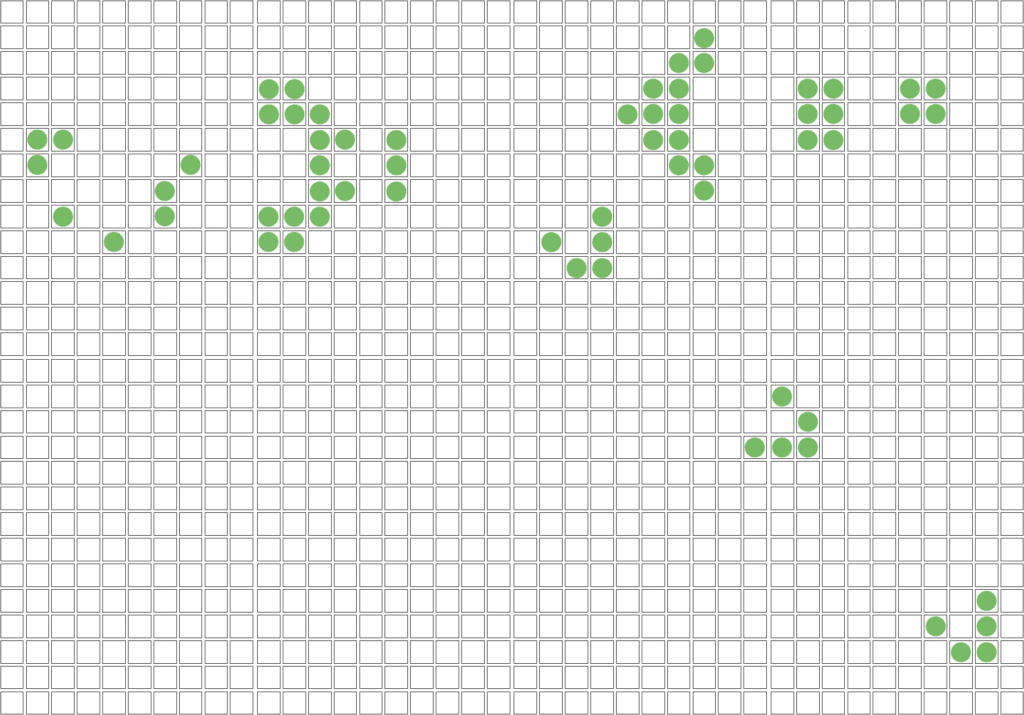
After several more cycles, we see there’s an infinite stream of gliders:

The glider gun also enables advanced computation. Since Gliders can carry information and interact, multiple guns can simulate logic gates. This leads to the realization that the Game of Life is Turing complete, capable of universal computation using only cell updates. In fact, it’s been proven that the Game of Life is capable of universal computation with the right setup, thus it is Turing complete.
4. Key Learnings From Conway’s Game of Life
Conway’s Game of Life teaches several foundational ideas in computation and complexity science. One of the most important is emergent behavior. With only four rules, the system creates rich dynamics.
Another is sensitivity to initial conditions. Tiny changes in the starting grid can lead to completely different outcomes. For example, a glider gun may fail if just one cell is removed, preventing the emission of gliders.
The game also illustrates how local interactions lead to global patterns. Each cell only “knows” about its neighbors, yet large-scale patterns can emerge. This insight applies to urban planning, neural networks, and swarm intelligence.
5. Conclusion
In this article, we learned how Conway’s Game of Life uses simple rules to simulate complex, lifelike systems.
The game demonstrates how simple, local rules can lead to unexpected global complexity and how systems can self-organize and evolve. Cell patterns offer glimpses into foundational concepts in artificial life, computation, and complexity theory. The post Conway’s Game of Life first appeared on Baeldung on Computer Science.
Content mobilized by FeedBlitz RSS Services, the premium FeedBurner alternative. |